No, human brains are not more efficient than computers

Epistemic status: grain of salt. There's lots of uncertainty in how many FLOP/s the brain can perform.

In informal debate, I've regularly heard people say something like, "oh but brains are so much more efficient than computers" (followed by a variant of "so we shouldn't worry about AGI yet"). Putting aside the weakly argued AGI skepticism, brains actually aren't all that much more efficient than computers (at least not in any way that matters).

The first problem is that these people are usually comparing the energy requirements of training large AI models to the power requirements of running the normal waking brain. These two things don't even have the same units.

The only fair comparison is between the trained model and the waking brain or between training the model and training the brain. Training the brain is called evolution, and evolution isn't particularly known for its efficiency.

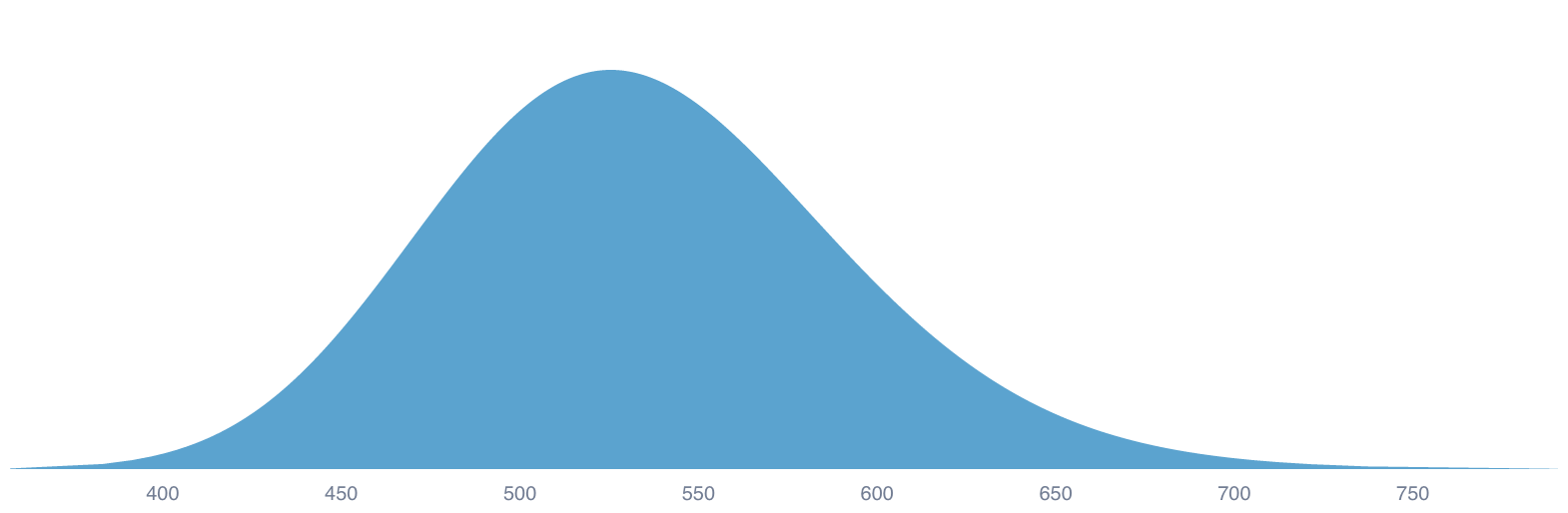
Let's start with the easier comparison: a trained model vs. a trained brain. Joseph Carlsmith estimates that the brain delivers roughly $1$ petaFLOP/s (=$10^{15}$ floating-point operations per second)¹. If you eat a normal diet, you're expending roughly $10^{-13}$ J/FLOP.

Meanwhile, the supercomputer Fugaku delivers $450$ petaFLOP/s at $30$ MW, which comes out to about $10^{-11.5}$ J/FLOP…. So I was wrong? Computers require almost $500$ times more energy per FLOP than humans?

$\frac{\text{Supercomputer J}/\text{FLOP}}{\text{Human J} /\text{FLOP}}$

What this misses is an important practical point: supercomputers can tap pretty much directly into sunshine; human food calories are heavily-processed hand-me-downs. We outsource most of our digestion to mother nature and daddy industry.

Even the most whole-foods-grow-your-own-garden vegan is $2$-$3$ orders of magnitude less efficient at capturing calories from sunlight than your average device². That's before animal products, industrial processing, or any of the other Joules it takes to run a modern human.

After this correction, humans and computers are about head-to-head in energy/FLOP, and it's only getting worse for us humans. The fact that the brain runs on so little actual juice suggests there's plenty of room left for us to explore specialized architectures, but it isn't the damning case many think it is. (We're already seeing early neuromorphic chips out-perform neurons' efficiency by four orders of magnitude.)

$\frac{\text{Electronic efficiency}}{\text{Biological efficiency}}$

But what about training neural networks? Now that we know the energy costs per FLOP are about equal, all we have to do is compare FLOPs required to evolve brains to the FLOPs required to train AI models. Easy, right?

Here's how we'll estimate this:

1. For a given, state-of-the-art NN (e.g., GPT-3, PaLM), determine how many FLOP/s it performs when running normally.
2. Find a real-world brain which performs a similar number of FLOP/s.
3. Determine how long that real-world brain took to evolve.
4. Compare the number of FLOPs (not FLOP/s) performed during that period to the number of FLOPs required to train the given AI.

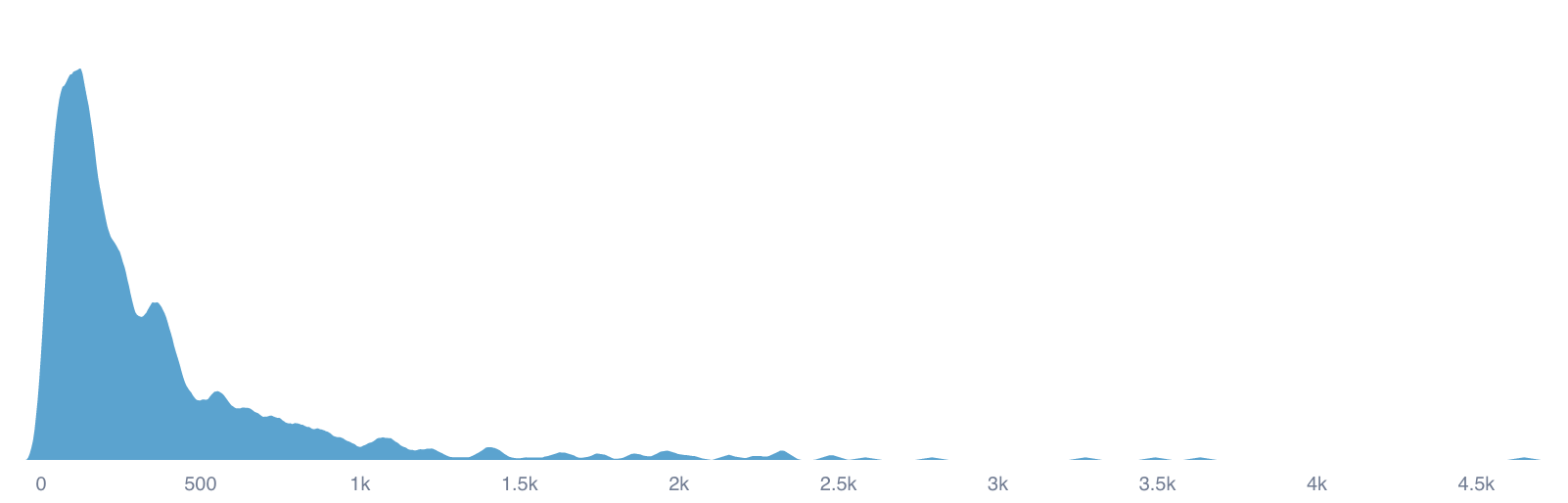
Fortunately, we can piggyback off the great work done by Ajeya Cotra on forecasting "Transformative" AI. She calculates that GPT-3 performs about $10^{12}$ FLOP/s³, or about as much as a bee.

Going off Wikipedia, social insects evolved only about 150 million years ago. That translates to between $10^{38}$ and $10^{44}$ FLOPs. GPT-3, meanwhile, took about $10^{23.5}$ FLOPs. That means evolution is $10^{15}$ to $10^{22}$ times less efficient.

$\log_{10}\left(\text{total FLOPs to evolve bee brains}\right)$

Now, you may have some objections. You may consider bees to be significantly more impressive than GPT-3. You may want to select a reference animal that evolved earlier in time. You may want to compare unadjusted energy needs. You may even point out the fact that the Chinchilla results suggest GPT-3 was "significantly undertrained".

Object all you want, and you still won't be able to explain away the >$15$ OOM gap between evolution and gradient descent. This is no competition.

What about other metrics besides energy and power? Consider that computers are about 10 million times faster than human brains. Or that if the human brain can store a petabyte of data, S3 can do so for about $20,000 (2022). Even FLOP for FLOP, supercomputers already underprice humans.⁴ There's less and less for us to brag about it.

$\frac{\$/(\text{Human FLOP/s})}{\$/(\text{Supercomputer FLOP}/s)}$

Brain are not magic. They're messy wetware, and hardware will catch up has caught up.

Postscript: brains actually might be magic. Carlsmith assigns less than 10% (but non-zero) probability that the brain computes more than $10^{21}$ FLOP/s. In this case, brains would currently still be vastly more efficient, and we'd have to update in favor of additional theoretical breakthroughs before AGI.

If we include the uncertainty in brain FLOP/s, the graph looks more like this:

$\frac{\text{Supercomputer J}/\text{FLOP}}{\text{Human J} /\text{FLOP}}$

(With a mean of ~$10^{19}$ and median of $830$.)

Appendix

Squiggle snippets used to generate above graphs. (Used in conjunction with obsidian-squiggle).

brainEnergyPerFlop = {
	humanBrainFlops = 15; //10 to 23;	// Median 15; P(>21) < 10%
	humanBrainFracEnergy = 0.2;
	humanEnergyPerDay = 8000 to 10000; // Daily kJ consumption
	humanBrainPower = humanEnergyPerDay / (60 * 60 * 24); // kW
	humanBrainPower * 1000 / (10 ^ humanBrainFlops) // J / FLOP
}

supercomputerEnergyPerFlop = {
    // https://www.top500.org/system/179807/ 
	power = 25e6 to 30e6; // J
	flops = 450e15 to 550e15;
	power / flops
}

supercomputerEnergyPerFlop / brainEnergyPerFlop

humanFoodEfficiency = {
	photosynthesisEfficiency = 0.001 to 0.03
	trophicEfficiency = 0.1 to 0.15
	photosynthesisEfficiency * trophicEfficiency 
}

computerEfficiency = {
    solarEfficiency = 0.15 to 0.20
    transmissionEfficiency = 1 - (0.08 to .15)
    solarEfficiency * transmissionEfficiency
}

computerEfficiency / humanFoodEfficiency

evolution = {
    // Based on Ayeja Cotra's "Forecasting TAI with biological anchors"
    // All calculations are in log space.
	
	secInYear = log10(365 * 24 * 60 * 60);
	
	// We assume that the average ancestor pop. FLOP per year is ~constant.
	// cf. Humans at 10 to 20 FLOP/s & 7 to 10 population
	ancestorsAveragePop = uniform(19, 23); # Tomasik estimates ~1e21 nematodes
    ancestorsAverageBrainFlops = 2 to 6; // ~ C. elegans
	ancestorsFlopPerYear = ancestorsAveragePop + ancestorsAverageBrainFlops + secInYear;

	years = log10(850e6) // 1 billion years ago to 150 million years ago
	ancestorsFlopPerYear + years
}

humanLife$ = 1e6 to 10e6
humanBrainFlops = 1e15
humanBrain$PerFlops = humanLife$ / humanBrainFlops 

supercomputer$ = 1e9
supercomputerFlops = 450e15
supercomputer$PerFlop = supercomputer$ / supercomputerFlops


supercomputer$PerFlops/humanBrain$PerFlops

Footnotes

1. Watch out for FLOP/s (floating point operations per second) vs. FLOPs (floating point operations). I'm sorry for the source of confusion, but FLOPs usually reads better than FLOP. ↩

2. Photosynthesis has an efficiency around 1%, and jumping up a trophic level means another order of magnitude drop. The most efficient solar panels have above 20% efficiency, and electricity transmission loss is around 10%. ↩

3. Technically, it's FLOP per "subjective second" — i.e., a second of equivalent natural thought. This can be faster or slower than "truth thought." ↩

4. Compare FEMA's value of a statistical life at $7.5 million to the $1 billion price tag of the Fukuga supercomputer, and we come out to the supercomputer being a fourth the cost per FLOP. ↩