MNIST-CIFAR Dominoes

Here are some dominoes based on [1]. The idea behind this dataset is that there are two "patterns" in the data: the MNIST image and the CIFAR image.

Pasted image 20230316175757.png

Notice that some of the dominoes have only one "pattern" present. By tracking training/test loss on these one-sided dominoes, we can tease apart how quickly the model learns the two different patterns.

We'd like to compare these pattern-learning curves to the curves predicted by the toy model of [2]. In particular, we'd like to compare predictions to the empirical curves as we change the relevant macroscopic parameters (e.g., prevalence, reliability, and simplicity¹).

Which means running sweeps over these macroscopic parameters.

Prevalence

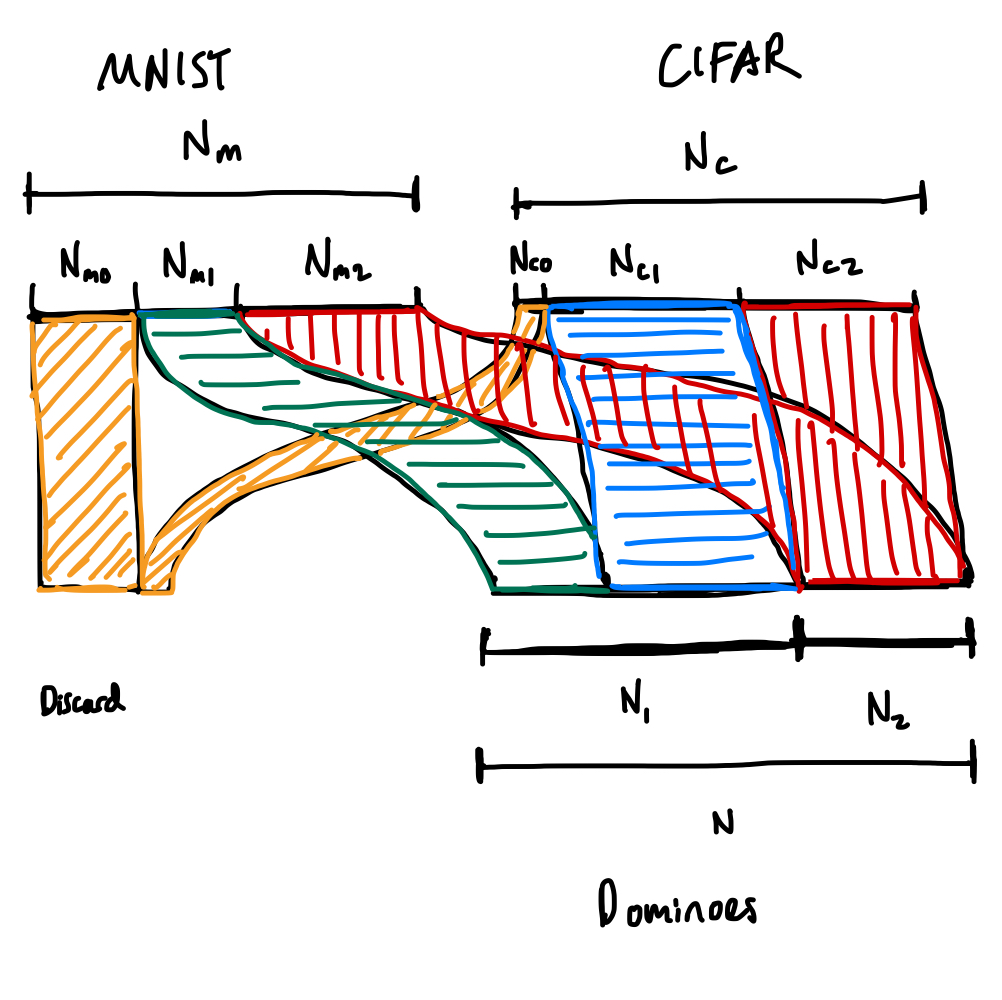
What happens as we change the relative incidence of MNIST vs CIFAR images in the dataset? We can accomplish this by varying the frequency of one-sided MNIST dominoes vs. one-sided CIFAR dominoes.

We control two parameters:

$p_m$ , the probability of a domino containing an MNIST image (either one-sided or two-sided),
$p_c$ , the probability of a domino containing a CIFAR image (either one-sided or two-sided), and

Two parameters are fixed by our datasets:

$N_m$ , the number of samples in the MNIST dataset.
$N_c$ , the number of samples in the CIFAR dataset.

Given these parameters, we have to determine:

$r_{m0}$ , the fraction of the MNIST dataset that we reject,
$r_{m1}$ , the fraction of the MNIST dataset that ends up in one-sided dominoes,
$r_{m2}$ , the fraction of the MNIST dataset that ends up in two-sided dominoes,

and, similarly, $r_{c0}$ , $r_{c1}$ , and $r_{c2}$ for the CIFAR dataset.

Here's the corresponding Sankey diagram (in terms of numbers of samples rather than probabilities, but it's totally equivalent).

Six unknowns means we need six constraints.

We get the first two from the requirement that probabilities are normalized,

r_{m0} + r_{m1} + r_{m2} = r_{c0} + r_{c1} + r_{c2} = 1,

and the another from the double dominoes requiring the sample number of samples from both datasets,

r_{m2} N_m = r_{c2} N_c.

Out of convenience, we'll introduce an additional variable, which we immediately constrain,

N = r_{c1}N_c + r_{m1}N_m + r_{m2} N_m,

the number of samples in the resulting dominoes dataset.

We get the last three constraints from our choices of $p_{m}$ , $p_c$ , and $p_1$ :

N p_m = N_{m1} + N_2 = r_{m1} N_m + r_{m2} N_m,

N p_c = N_{c1} + N_2 = r_{c1} N_c + r_{c2} N_c,

In matrix format,

\begin{pmatrix} 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & N_m & 0 & 0 & -N_c & 0 \\ 0 & N_m & N_m & 0 & N_c & 0 & 1 \\ 0 & N_m & N_m & 0 & 0 & 0 & -p_m \\ 0 & 0 & 0 & 0 & N_c & N_c & -p_c \\ 0 & N_m & 0 & 0 & N_c & 0 & -p_1 \end{pmatrix} \cdot \begin{pmatrix} r_{m0} \\ r_{m1} \\ r_{m2} \\ r_{c0} \\ r_{c1} \\ r_{c2} \\ N \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix},

where $p_1 = 2 - p_c - p_m$ .

So unfortunately, this yields trivial answers where $r_{m0}=r_{c0}=1$ and all other values are 0. The solution seems to be to just allow there to be empty dominoes.

Reliability

We can vary the reliability by inserting "wrong" dominoes. I.e.: with some probability make either of the two sides display the incorrect class for the label.

Simplicity

One of the downsides of this task is that we don't have much control over the simplicity of the feature. MNIST is simpler than CIFAR, sure, but how much? How might we control this?

Axes conceived by Ekdeep Singh Lubana. ↩

MNIST-CIFAR Dominoes

Prevalence

Reliability

Simplicity

Footnotes