Research
Check out Timaeus's research for more work from my team.
Influence Dynamics and Stagewise Data Attribution
Current training data attribution (TDA) methods treat the influence one sample has on another as static, but neural networks learn in distinct stages that exhibit changing patterns of influence. In this work, we introduce a framework for stagewise data attribution grounded in singular learning theory. We predict that influence can change non-monotonically, including sign flips and sharp peaks at developmental transitions. We first validate these predictions analytically and empirically in a toy model, showing that dynamic shifts in influence directly map to the model's progressive learning of a semantic hierarchy. Finally, we demonstrate these phenomena at scale in language models, where token-level influence changes align with known developmental stages.
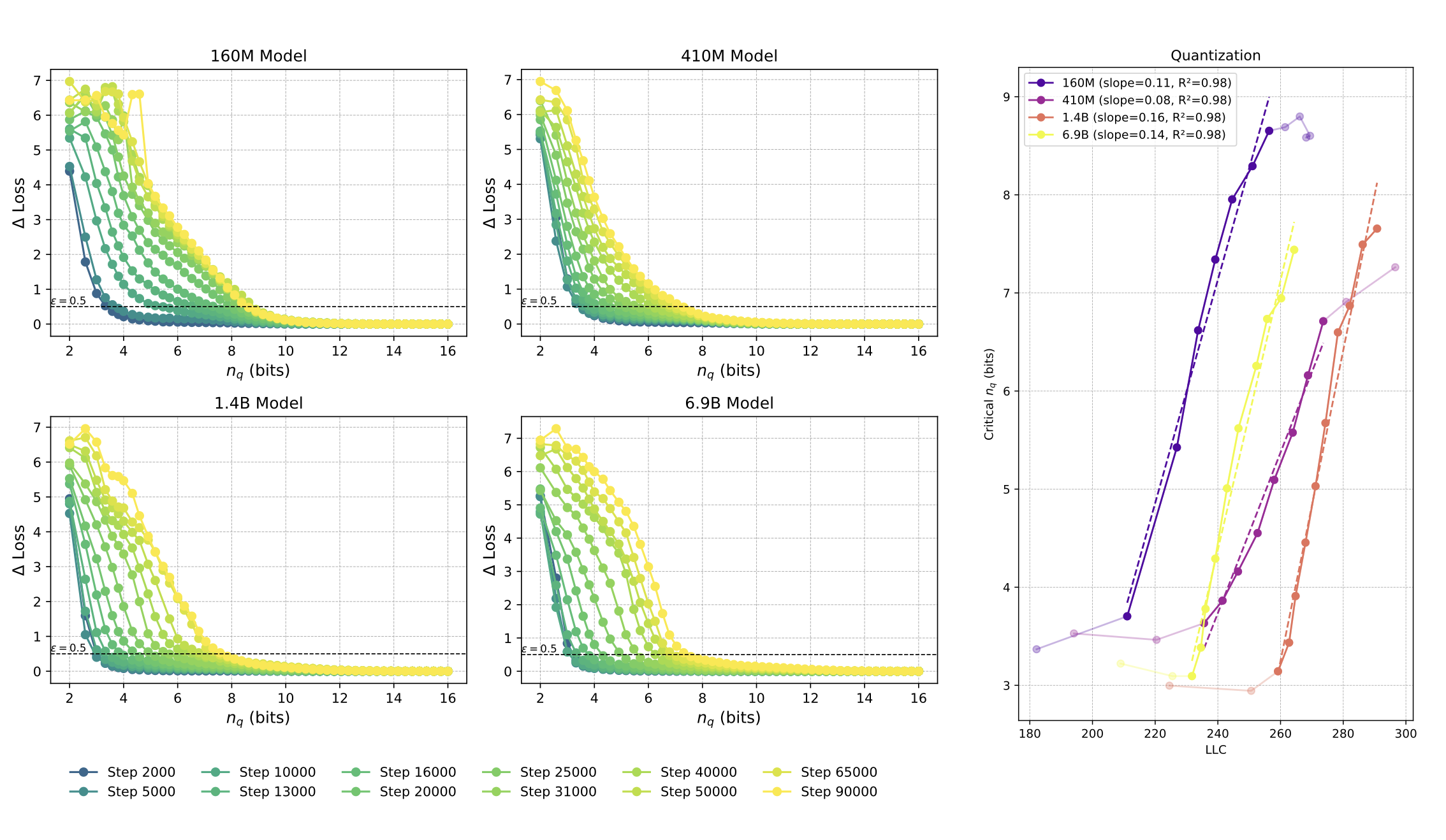
Compressibility Measures Complexity: Minimum Description Length Meets Singular Learning Theory
We study neural network compressibility by using singular learning theory to extend the minimum description length (MDL) principle to singular models like neural networks. Through extensive experiments on the Pythia suite with quantization, factorization, and other compression techniques, we find that complexity estimates based on the local learning coefficient (LLC) are closely, and in some cases, linearly correlated with compressibility. Our results provide a path toward rigorously evaluating the limits of model compression.
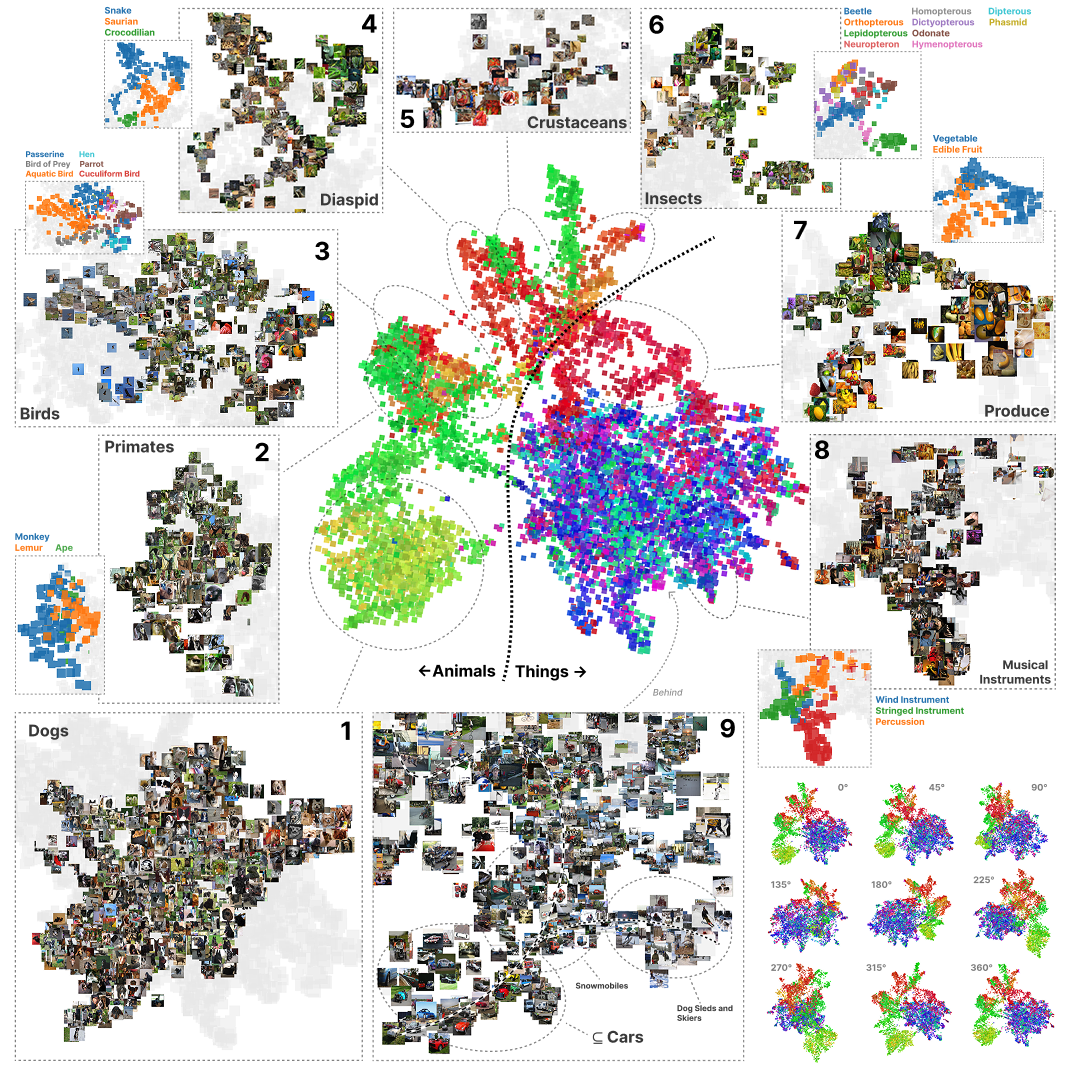
The Loss Kernel: A Geometric Probe for Deep Learning Interpretability
We introduce the loss kernel, an interpretability method for measuring similarity between data points according to a trained neural network. The kernel is the covariance matrix of per-sample losses computed under a distribution of low-loss-preserving parameter perturbations. We first validate our method on a synthetic multitask problem, showing it separates inputs by task as predicted by theory. We then apply this kernel to Inception-v1 to visualize the structure of ImageNet, and we show that the kernel's structure aligns with the WordNet semantic hierarchy. This establishes the loss kernel as a practical tool for interpretability and data attribution.
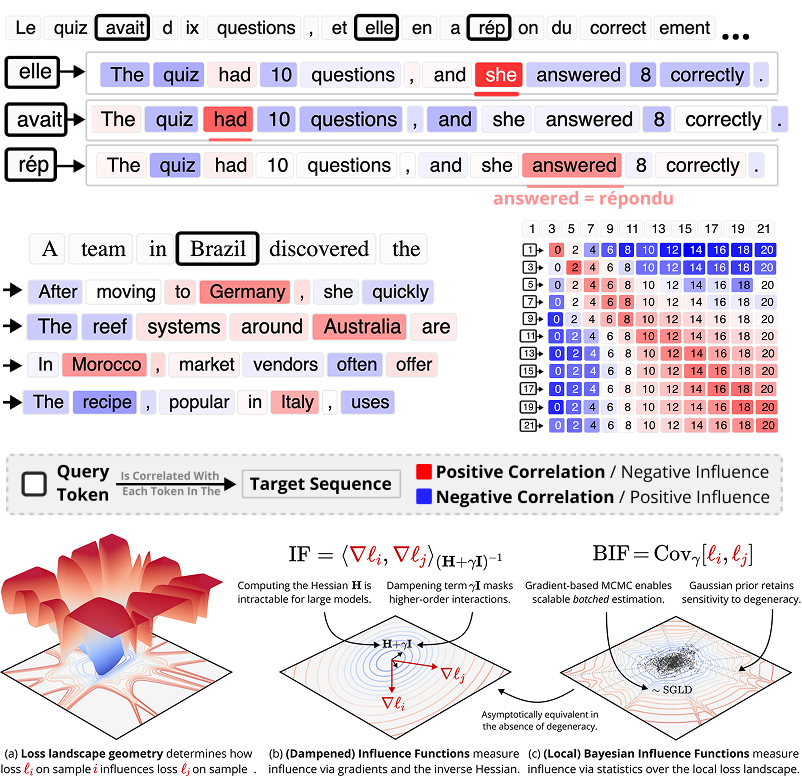
Bayesian Influence Functions for Hessian-Free Data Attribution
Classical influence functions face significant challenges when applied to deep neural networks, primarily due to non-invertible Hessians and high-dimensional parameter spaces. We propose the local Bayesian influence function (BIF), an extension of classical influence functions that replaces Hessian inversion with loss landscape statistics that can be estimated via stochastic-gradient MCMC sampling. This Hessian-free approach captures higher-order interactions among parameters and scales efficiently to neural networks with billions of parameters. We demonstrate state-of-the-art results on predicting retraining experiments.
Studying Small Language Models with Susceptibilities
We develop a linear response framework for interpretability that treats a neural network as a Bayesian statistical mechanical system. A small, controlled perturbation of the data distribution, for example shifting the Pile toward GitHub or legal text, induces a first-order change in the posterior expectation of an observable localized on a chosen component of the network. The resulting susceptibility can be estimated efficiently with local SGLD samples and factorizes into signed, per-token contributions that serve as attribution scores. Building a set of perturbations (probes) yields a response matrix whose low-rank structure separates functional modules such as multigram and induction heads in a 3M-parameter transformer. Susceptibilities link local learning coefficients from singular learning theory with linear-response theory, and quantify how local loss landscape geometry deforms under shifts in the data distribution.
You Are What You Eat – AI Alignment Requires Understanding How Data Shapes Structure and Generalisation
In this position paper, we argue that understanding the relation between structure in the data distribution and structure in trained models is central to AI alignment. First, we discuss how two neural networks can have equivalent performance on the training set but compute their outputs in essentially different ways and thus generalise differently. For this reason, standard testing and evaluation are insufficient for obtaining assurances of safety for widely deployed generally intelligent systems. We argue that to progress beyond evaluation to a robust mathematical science of AI alignment, we need to develop statistical foundations for an understanding of the relation between structure in the data distribution, internal structure in models, and how these structures underlie generalisation.
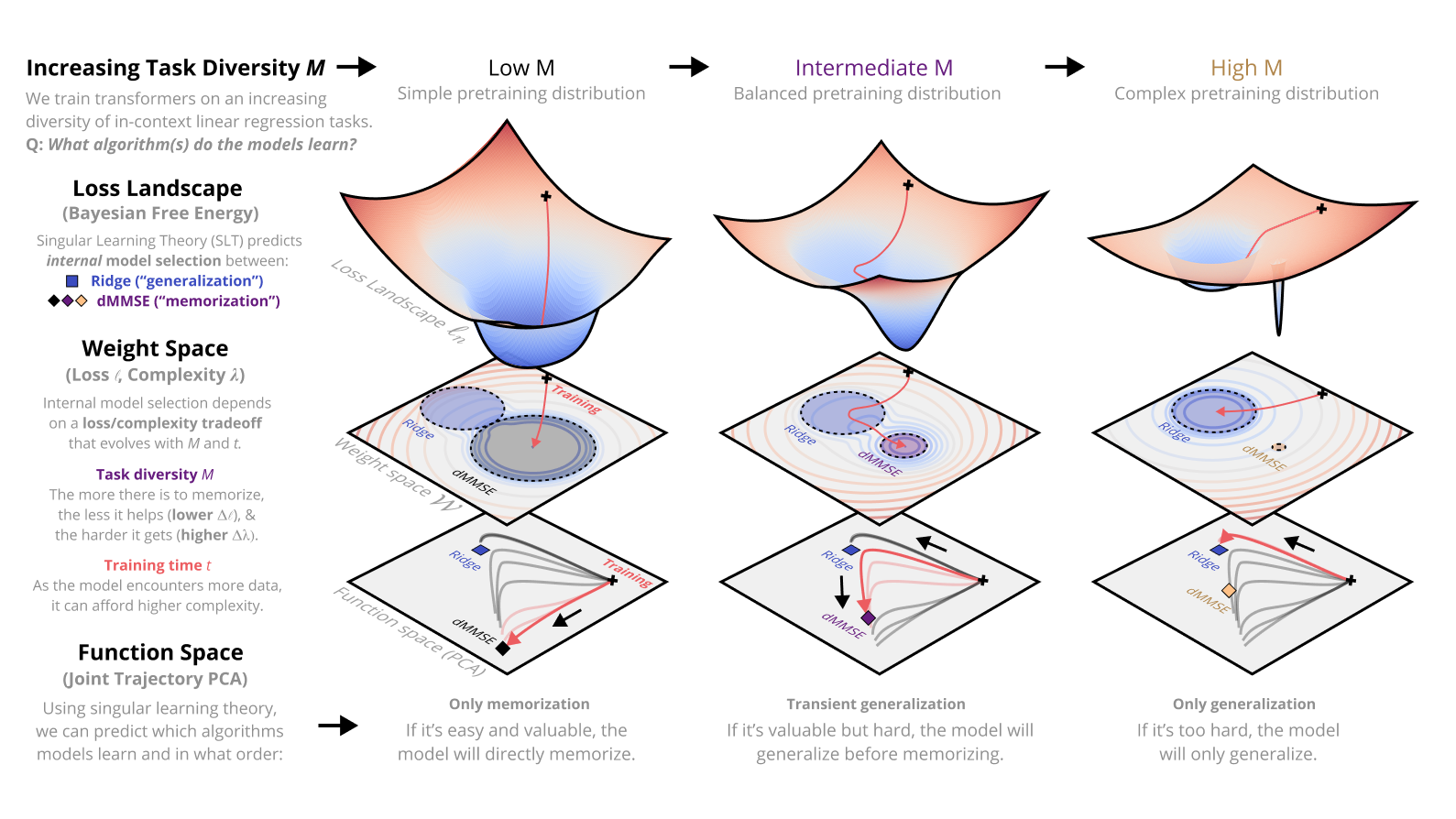
Dynamics of Transient Structure in In-Context Linear Regression Transformers
Modern deep neural networks display striking examples of rich internal computational structure. Uncovering principles governing the development of such structure is a priority for the science of deep learning. In this paper, we explore the transient ridge phenomenon: when transformers are trained on in-context linear regression tasks with intermediate task diversity, they initially behave like ridge regression before specializing to the tasks in their training distribution. This transition from a general solution to a specialized solution is revealed by joint trajectory principal component analysis. Further, we draw on the theory of Bayesian internal model selection to suggest a general explanation for the phenomena of transient structure in transformers, based on an evolving tradeoff between loss and complexity. We empirically validate this explanation by measuring the model complexity of our transformers as defined by the local learning coefficient.
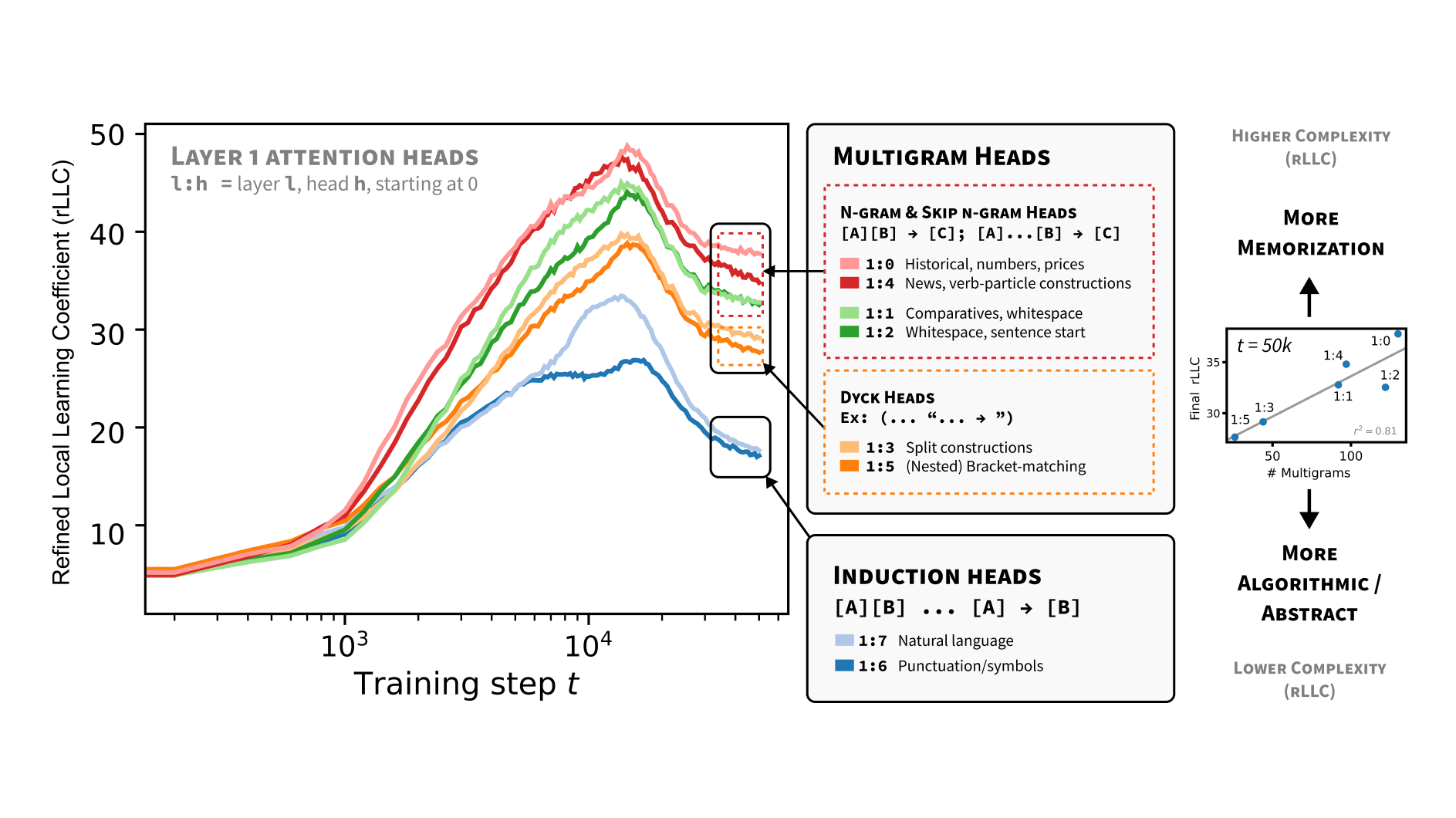
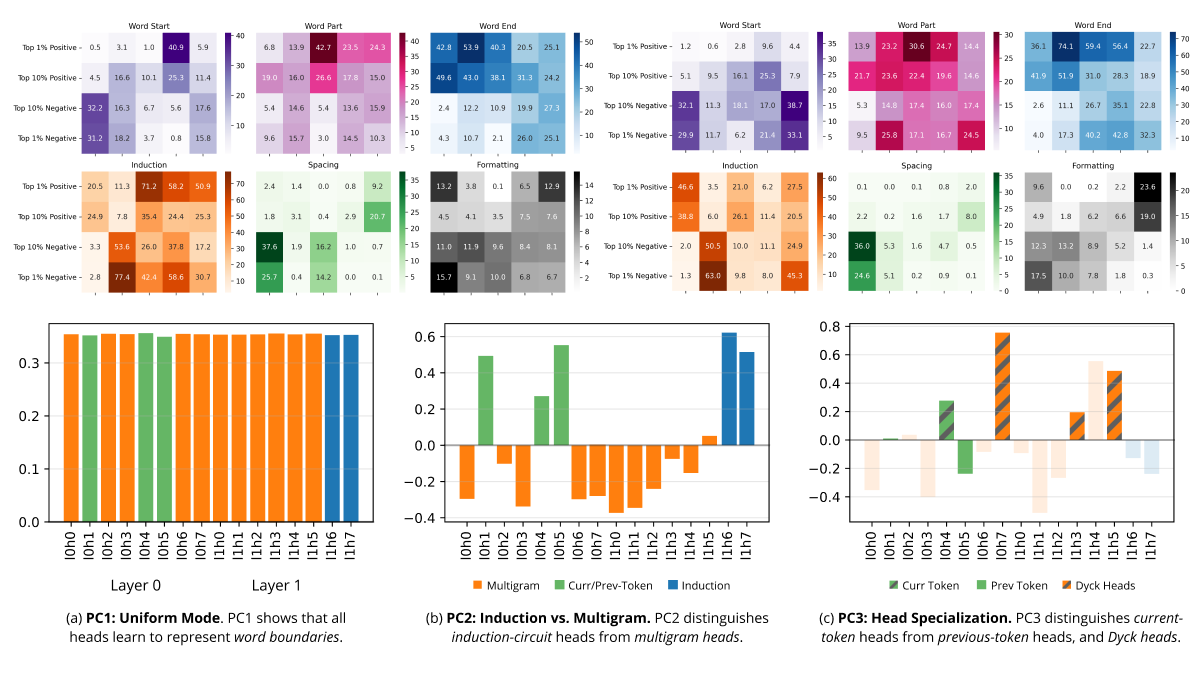
Differentiation and Specialization of Attention Heads via the Refined Local Learning Coefficient
We introduce refined variants of the Local Learning Coefficient (LLC), a measure of model complexity grounded in singular learning theory, to study the development of internal structure in transformer language models during training. By applying these refined LLCs (rLLCs) to individual components of a two-layer attention-only transformer, we gain novel insights into the progressive differentiation and specialization of attention heads. Our methodology reveals how attention heads differentiate into distinct functional roles over the course of training, analyzes the types of data these heads specialize to process, and discovers a previously unidentified multigram circuit. These findings demonstrate that rLLCs provide a principled, quantitative toolkit for developmental interpretability, which aims to understand models through their evolution across the learning process. More broadly, this work takes a step towards establishing the correspondence between data distributional structure, geometric properties of the loss landscape, learning dynamics, and emergent computational structures in neural networks.
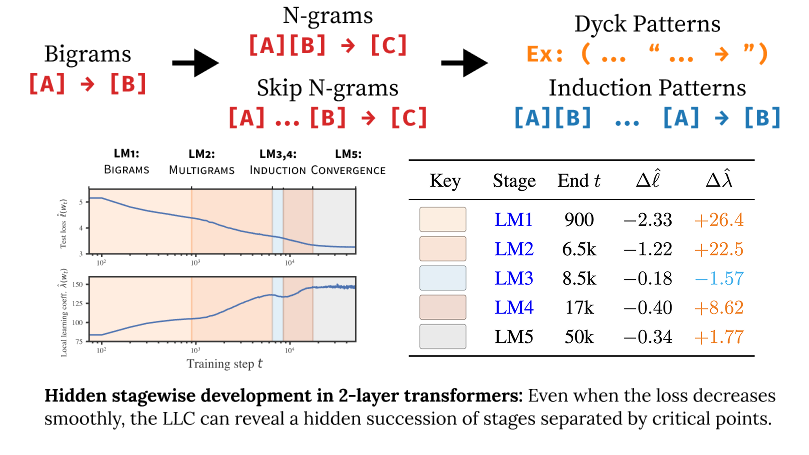
Loss Landscape Degeneracy Drives Stagewise Development in Transformers
We show that in-context learning emerges in transformers in discrete developmental stages, when they are trained on either language modeling or linear regression tasks. We introduce two methods for detecting the milestones that separate these stages, by probing the geometry of the population loss in both parameter space and function space. We study the stages revealed by these new methods using a range of behavioral and structural metrics to establish their validity.