This is an link post, originally posted at https://www.lesswrong.com/posts/HtxLbGvD7htCybLmZ/singularities-against-the-singularity-announcing-workshop-on.

This is an link post, originally posted at https://www.lesswrong.com/posts/zuYRyC3zghzgXLpEW/empirical-risk-minimization-is-fundamentally-confused.

Here are some dominoes based on [1]. The idea behind this dataset is that there are two "patterns" in the data: the MNIST image and the CIFAR image.

Notice that some of the dominoes have only one "pattern" present. By tracking training/test loss on these one-sided dominoes, we can tease apart how quickly the model learns the two different patterns.

We'd like to compare these pattern-learning curves to the curves predicted by the toy model of [2]. In particular, we'd like to compare predictions to the empirical curves as we change the relevant macroscopic parameters (e.g., prevalence, reliability, and simplicity¹).

Which means running sweeps over these macroscopic parameters.

Prevalence

What happens as we change the relative incidence of MNIST vs CIFAR images in the dataset? We can accomplish this by varying the frequency of one-sided MNIST dominoes vs. one-sided CIFAR dominoes.

We control two parameters:

• $p_m$, the probability of a domino containing an MNIST image (either one-sided or two-sided),
• $p_c$, the probability of a domino containing a CIFAR image (either one-sided or two-sided), and

Two parameters are fixed by our datasets:

• $N_m$, the number of samples in the MNIST dataset.
• $N_c$, the number of samples in the CIFAR dataset.

Given these parameters, we have to determine:

• $r_{m0}$, the fraction of the MNIST dataset that we reject,
• $r_{m1}$, the fraction of the MNIST dataset that ends up in one-sided dominoes,
• $r_{m2}$, the fraction of the MNIST dataset that ends up in two-sided dominoes,

and, similarly, $r_{c0}$, $r_{c1}$, and $r_{c2}$ for the CIFAR dataset.

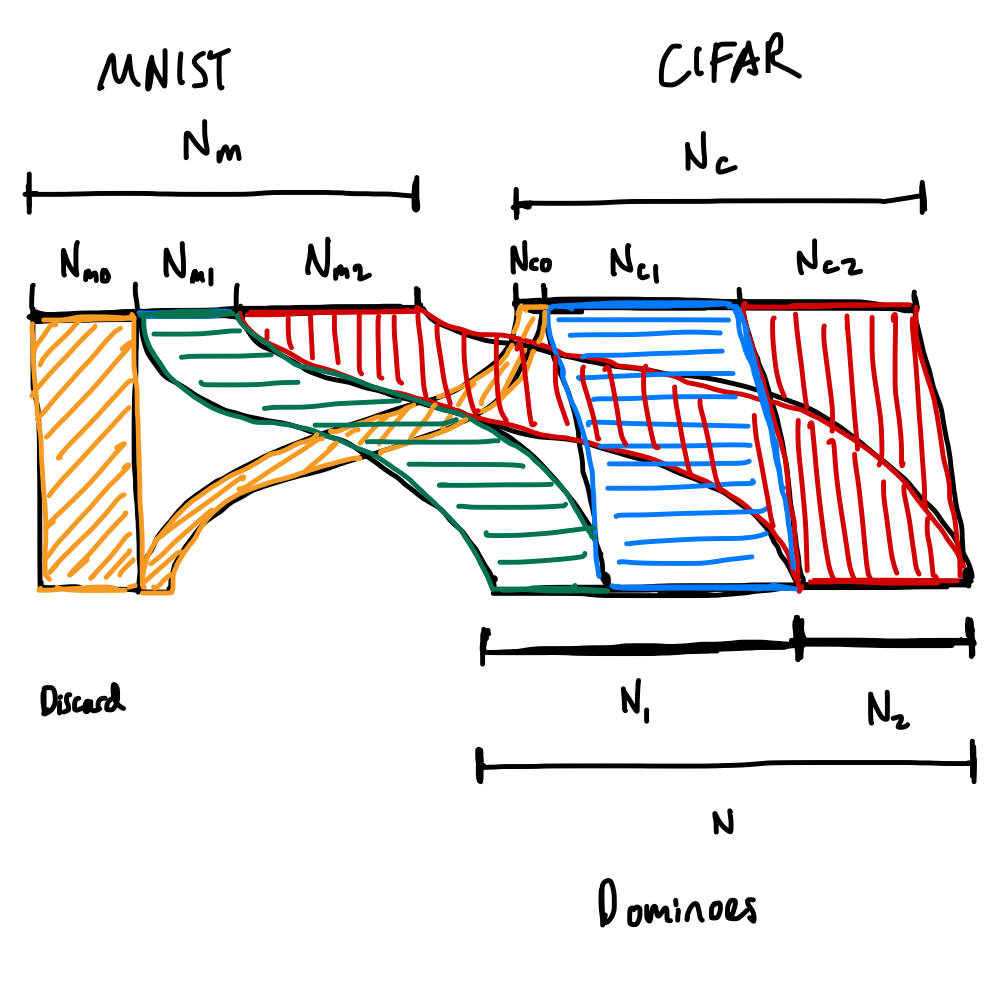Here's the corresponding Sankey diagram (in terms of numbers of samples rather than probabilities, but it's totally equivalent).

Six unknowns means we need six constraints.

We get the first two from the requirement that probabilities are normalized,

and the another from the double dominoes requiring the sample number of samples from both datasets,

Out of convenience, we'll introduce an additional variable, which we immediately constrain,

the number of samples in the resulting dominoes dataset.

We get the last three constraints from our choices of $p_{m}$, $p_c$, and $p_1$:

In matrix format,

where $p_1 = 2 - p_c - p_m$.

So unfortunately, this yields trivial answers where $r_{m0}=r_{c0}=1$ and all other values are 0. The solution seems to be to just allow there to be empty dominoes.

Reliability

We can vary the reliability by inserting "wrong" dominoes. I.e.: with some probability make either of the two sides display the incorrect class for the label.

Simplicity

One of the downsides of this task is that we don't have much control over the simplicity of the feature. MNIST is simpler than CIFAR, sure, but how much? How might we control this?

Produced as part of the SERI ML Alignment Theory Scholars Program - Winter 2022 Cohort

Most results under the umbrella of "deep learning theory" are not actually deep, about learning, or even theories.

This is because classical learning theory makes the wrong assumptions, takes the wrong limits, uses the wrong metrics, and aims for the wrong objectives. Learning theorists are stuck in a rut of one-upmanship, vying for vacuous bounds that don't say anything about any systems of actual interest.

Yudkowsky tweeting about statistical learning theorists. (Okay, not really.)

In particular, I'll argue throughout this sequence that:

• Empirical risk minimization is the wrong framework, and risk is a weak foundation.
• In approximation theory, the universal approximation results are too general (they do not constrain efficiency) while the "depth separation" results meant to demonstrate the role of depth are too specific (they involve constructing contrived, unphysical target functions).
• Generalization theory has only two tricks, and they're both limited:
  • Uniform convergence is the wrong approach, and model class complexities (VC dimension, Rademacher complexity, and covering numbers) are the wrong metric. Understanding deep learning requires looking at the microscopic structure within model classes.
  • Robustness to noise is an imperfect proxy for generalization, and techniques that rely on it (margin theory, sharpness/flatness, compression, PAC-Bayes, etc.) are oversold.
• Optimization theory is a bit better, but training-time guarantees involve questionable assumptions, and the obsession with second-order optimization is delusional. Also, the NTK is bad. Get over it.
• At a higher level, the obsession with deriving bounds for approximation/generalization/learning behavior is misguided. These bounds serve mainly as political benchmarks rather than a source of theoretical insight. More attention should go towards explaining empirically observed phenomena like double descent (which, to be fair, is starting to happen).

That said, there are new approaches that I'm more optimistic about. In particular, I think that singular learning theory (SLT) is the most likely path to lead to a "theory of deep learning" because it (1) has stronger theoretical foundations, (2) engages with the structure of individual models, and (3) gives us a principled way to bridge between this microscopic structure and the macroscopic properties of the model class¹. I expect the field of mechanistic interpretability and the eventual formalism of phase transitions and "sharp left turns" to be grounded in the language of SLT.

Why theory?

A mathematical theory of learning and intelligence could form a valuable tool in the alignment arsenal, that helps us:

• Develop and scale interpretability tools
• Inspire better experiments (i.e., focus our bits of attention more effectively).
• Establish a common language between experimentalists and theorists.

That's not to say that the right theory of learning is risk-free:

• A good theory could inspire new capabilities. We didn't need a theory of mechanics to build the first vehicles, but we couldn't have gotten to the moon without it.
• The wrong theory could mislead us. Just as theory tells us where to look, it also tells us where not to look. The wrong theory could cause us to neglect important parts of the problem.
• It could be one prolonged nerd-snipe that draws attention and resources away from other critical areas in the field. Brilliant string theorists aren't exactly helping advance living and technology standards by computing the partition functions of black holes in 5D de-Sitter spaces.²

All that said, I think the benefits currently outweigh the risks, especially if we put the right infosec policy in place when if learning theory starts showing signs of any practical utility. It's fortunate, then, that we haven't seen those signs yet.

Outline

My aims are:

• To discourage other alignment researchers from wasting their time.
• To argue for what makes singular learning theory different and why I think it the likeliest contender for an eventual grand unified theory of learning.
• To invoke Cunningham's law — i.e., to get other people to tell me where I'm wrong and what I've been missing in learning theory.

There's also the question of integrity: if I am to criticize an entire field of people smarter than I am, I had better present a strong argument and ample evidence.

Throughout the rest of this sequence, I'll be drawing on notes I compiled from lecture notes by Telgarsky, Moitra, Grosse, Mossel, Ge, and Arora, books by Roberts et al. and Hastie et al., a festschrift of Chervonenkis, and a litany of articles.³

The sequence follows the three-fold division of approximation, generalization, and optimization preferred by the learning theorists. There's an additional preface on why empirical risk minimization is flawed (up next) and an epilogue on why singular learning theory seems different.

• 0. The shallow reality of 'deep learning theory' (You are here)
• 1. Empirical risk minimization is fundamentally confused
• 2. Approximation is expensive, but the lunch is cheap
• 3. On generalization— against PAC-learning
• 4. On optimization— the NTK is bad, actually
• 5. What makes singular learning theory different?

This is an link post, originally posted at https://www.lesswrong.com/posts/BDTfddkttFXHqGnEi/the-shallow-reality-of-deep-learning-theory.